Imagine playing Pac-Man – you control the yellow character, navigating through a maze, eating pellets while avoiding ghosts. As a human player, you're making decisions based on what you see and trying to maximize your score. Reinforcement Learning (RL) agents work similarly, but they're computer programs that learn to play games or solve problems through trial and error, just like how you might get better at Pac-Man with practice.
An agent in reinforcement learning is essentially a decision-maker – it's the "brain" that chooses what actions to take in any given situation. The agent is constantly learning from its experiences, getting better at making decisions that lead to higher rewards over time. This approach is fundamentally different from traditional programming where we explicitly tell computers what to do; instead, RL agents figure out the best strategies by themselves through interaction with their environment.
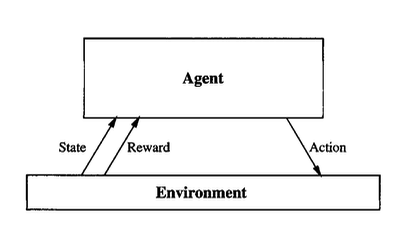
Figure 1: Basic reinforcement learning agent-environment interaction diagram
The Core Components of Reinforcement Learning
The Agent-Environment Interaction Loop
At the heart of reinforcement learning lies a simple but powerful concept: the agent-environment interaction loop. This continuous cycle forms the foundation of how RL agents learn and make decisions. Let's break down each component using our Pac-Man example.
Understanding the Environment
The environment is everything with. In Pac-Man, the environment includes the maze layout, the positions of pellets, the locations and movements of ghosts, and the current score. The environment responds to the agent's actions by changing state and providing feedback in the form of rewards. Think of the environment as the "world" in which the agent operates. It's important to note that the agent cannot directly control the environment – it can only influence it through its actions. Just like in Pac-Man, you can't move the walls or control where the ghosts go initially, but your movements affect the game state.

Figure 2: Pac-man game environment showing agent, ghosts, and pellets
States: The Agent's Perception of the World
A state represents the current situation or configuration of the environment that the agent observes. In Pac-Man, a state might include:
- Pac-Man's position
- Ghost positions
- Pellet status
- Power pellet activity
- Score
Mathematically, we can represent the state space as S, which contains all possible states the agent might encounter. The current state at time t is denoted as s_t.
For example, if Pac-Man is at position (5,3) in the maze, with ghosts at positions (2,1), (8,6), (4,9), and (7,2), and there are 180 pellets remaining, this entire configuration represents one specific state.
Actions: The Choices Available
Actions are the decisions or moves that an agent can make in any given state. In Pac-Man, the action space A is relatively simple:
- Move Up
- Move Down
- Move Left
- Move Right
- Stay Still (if supported)
The action taken at time t is denoted as a_t. It's crucial to understand that the set of available actions might change depending on the current state. For instance, if Pac-Man is next to a wall, moving in that direction might not be a valid action.
Rewards: The Learning Signal
Rewards are numerical values that the environment gives to the agent after each action, indicating how good or bad that action was. The reward function R(s, a, s') specifies what reward the agent receives for taking action a in state s and transitioning to states'.
In Pac-Man, the reward structure might look like:
- +10: Regular pellet
- +50: Power pellet
- +200: Eat ghost while powered
- -500: Caught by ghost
- +1000: Clear all pellets
- -1: Each move (efficiency penalty)
The key insight is that rewards provide the learning signal – they tell the agent which actions lead to desirable outcomes and which should be avoided.
Policy: The Agent’s Strategy
A policy is the strategy or set of rules that determines what action the agent should take in any given state. Think of it as the agent's "brain" or decision-making process. The policy is denoted as π (pi) and can be written as π(s) for deterministic policies or π(a|s) for stochastic policies.
Deterministic vs. Stochastic Policies
Deterministic policies always choose the same action for a given state. For example, a simple Pac-Man policy might be: "If there's a pellet to the right, always move right."
Stochastic policies assign probabilities to different actions. A more sophisticated policy might say: "If there's a pellet to the right, move right with 70% probability, but also consider other directions with lower probabilities to avoid getting trapped."
Mathematically, for a stochastic policy:
This means the probability of taking action a when in state s at time
t.
Example Policy in Pac-Man
Policy π:
- If ghost is adjacent and no power pellet active:
→ Move away from ghost (40% probability each for safe directions) - Else if power pellet available and ghost nearby:
→ Move toward power pellet (80% probability) - Else if pellet visible:
→ Move toward nearest pellet (60% probability) - Else:
→ Explore randomly (25% probability each direction)
The Q-Function: Estimating Action Values
The Q-function (Quality function) is one of the most important concepts in reinforcement learning. It estimates how good it is to take a specific action in a specific state, considering all future rewards the agent might receive.
Mathematical Definition
The Q-function is denoted as Q(s, a) and represents the expected cumulative reward for taking action a in state s and following the optimal policy thereafter:
Where:
- γ (gamma) is the discount factor (0 ≤ γ < 1)
- Rₜ₊₁ is the reward at time t+1
- E[] denotes expected value
Simple Example: Q-Values in Pac-Man
Let’s say Pac-Man is in a state where he's at position (3,2) and there are pellets in multiple directions. The Q-values might look like:
- Q((3,2), "Move Right") = 85 (leads to pellet + safe path)
- Q((3,2), "Move Left") = 30 (leads to dead end)
- Q((3,2), "Move Up") = -200 (ghost is there!)
- Q((3,2), "Move Down") = 60 (neutral space)
The agent would choose "Move Right" because it has the highest Q-value.
Conclusion: The Power of Learning Through Interaction
Reinforcement learning agents represent a powerful paradigm where artificial intelligence systems learn optimal behavior through trial-and-error interaction with their environment. Using Pac-Man as our example, we've seen how agents can start with no knowledge and gradually develop sophisticated strategies through the fundamental cycle of observation, action, reward, and learning.
The key concepts we've explored – agents, states, actions, rewards, policies, Q-functions. What makes reinforcement learning particularly exciting is its generality. The same principles that allow an agent to master Pac-Man can be applied to training robots, optimizing resource allocation, controlling autonomous vehicles, or even developing game-playing AIs that surpass human performance.
The journey from a randomly-moving Pac-Man to one that consistently achieves high scores mirrors the broader potential of reinforcement learning: turning uncertainty and exploration into mastery and optimal performance through the simple but powerful mechanism of learning from interaction with the world.
But we’re just getting started! In the next blog, we’ll dive into a real-world application—how we’re implementing reinforcement learning in Pixie to respond dynamically to user feedback, optimizing the system through real-time learning loops. Stay tuned; it’s about to get interactive.

